Rumus Menghitung Diagram Lingkaran - Diagram lingkaran sering di jumpai di berbagai soal dalam matematika. Pelajaran matematika sudah di dapatkan mulai dari bangku sekolah dasar dan diagram lingkaran mulain di pelajari di bangku sekolah menengah pertama. Pada kesempatan kali ini, kami akan membahas tentang diagram lingkaran, cara menghitung diagram lingkaran, rumus diagram lingkaran, rumus menghitung diagram lingkara, contoh soal diagram lingkaran, rumus diagram lingkaran biasa (dalam bnetuk angka), rumus diagram liangkaran dalam bentuk derajat, rumus diagram lingkaran dalam bentuk persen, teori perbandingan dan lain-lain. Semoga dengan membaca artikel kami ini anda lebih paham mengenai diagram lingkaran.
Diagram Lingkaran
Diagram lingkaran merupakan diagram yang menampilkan sebuh data atau hasil angka dalam bentuk lingkaran. Diagram sendiri terbagi atas beberapa jenis, diantaranya diagram batang, diagram garis, diagram lingkaran. Pada soal-soal matematika sering di gunakan diagram lingkaran untuk mengetahui perbandingan dari total jumlah yang diketahui. Biasanya diagram lingkaran digunakan untuk persentase, menentukan statistik, dan lain-lain. Berikut beberapa unsur diagram lingkaran, sebagai berikut:
Perhatikan Gambar berikut:
 |
| Gambar 1: |
Dari gambar diatas dapat di lihat bahwa data yang terdapat pada gambar adalah data A, data B, data C, dan data D. Semua data mempunyai batasan daerah yang membedakan besaran data atau jumlah pada masing-masing data. Untuk mencari besaran data atau berapa jumlah pada masing-masing data, terlebih dahulu harus di ketahui beberapa data. Ada beberapa jenis soal yang mungkin digunakan pada diagram lingkaran, diantaranya:
- Diagram lingkaran biasa (dalam bentuk angka)
- Diagram lingkaran dalam bentuk derajat (°)
- Diagram lingkaran dalam bentuk persen (%)
Rumus Diagram Lingkaran
Rumus yang digunakan dalam mencari nilai yang ditanyakan berbeda-beda pada diagram lingkran. Tergantung bunyi soalnya bagaimana, kami akan membahas secara terpisah sesuai contoh kasus soal yang sering di temui. Berikut beberapa rumus yang dapat di gunakan pada diagram lingkaran, diantaranya:
Rumus diagram lingkaran biasa (dalam bentuk angka)
Pada kasus diagram lingkaran biasa (dalam bentuk angka), anda dapat menghitungnya sesuai dengan rumus umum diagram lingkaran yang biasa di gunakan:
Rumus:
Jumalah data yang ditanyakan = total jumlah data - total data yang diketahui
Contoh soal
Sebuah kelas memiliki total siswa sebanya 42 siswa yang di bentuk dalam diagram lingkaran sebagai berikut:
Jika banyak siswa yang mengikuti kegiatan eskul yang dibentuk dalam diagram lingkaran seperti di atas. Berapakah jumlah siswa yang tidak mengikuti eskul sama sekali?
Jawab:
Diketahui:
Total siswa = 42 siswa
Eskul basket = 10 siswa
Eskul bola = 5 siswa
Eskul silat = 10 siswa
Ditanyakan:
Siswa yang tidak mengikuti eskul ... ?
Penyelesaian:
Rumus:
Jumalah data yang ditanyakan = total jumlah data - total data yang diketahui
Siswa yang tidak mengikuti eskul = total siswa - (eskul basket + eskul bola + eskul silat)
= 42 siswa - (10 siswa + 5 siswa + 10 siswa)
= 42 siswa - 25 siswa
= 17 siswa
Jadi, siswa yang tidak mengikuti eskul sama sekali adalah 17 siswa
Rumus Diagram Lingkaran dalam bentuk Derajat (°)
Pada kasus ini, data yang di ketahui berbentuk derajat. Untuk dapat mengetahui jumlah yang ditanyakan, pertama yang harus diketahui adalah jumlah derajat yang di tanyakan kemudian membaginya denga 360° (360° merupakan ketetapan lingkaran penuh) setelah itu kalikan dengan total jumlah nilai yang diketahui.
Rumus:
Nilai yang ditanyakan = (Jumlah sudut/360°) x total nilai
Contoh soal
Sebuah sekolah memiliki 1260 siswa. Di sekolah tersebut mengharuskan siswanya untuk ikut serta dalam kegiatan eskul. Jika siswa yang mengikuti eskul dibentuk dalam diagram lingkaran dalam bentuk derajat (°) sebagai berikut:
Berapakah jumlah siswa yang mengikuti esukul musik?
Jawab:
Diketahui:
total siswa = 1260 siswa
eskul basket = 130°
eskul bola = 100°
eskul silat = 80°
Ditanyakan:
Banyak siswa yang mengikuti eskul musik ... ?
Penyelesaian:
Pertama cari berapa derajat siswa yang mengikuti eskul musik,
eskul musik = 360° - (eskul basket + eskul bola + eskul silat)
= 360° - (130°-100°-80°)
= 360° - 310°
= 50°
Kemudian, gunakan rumus untuk mencari jumlah siswa yang mengikuti eskul musik:
Jumlas siswa eskul musik = (derajat eskul musik/360°) x total siswa
= (50°/360°) x 1260 siswa
= 63000/360
= 175 siswa
Jadi, jumlah siswa yang mengikuti eskul musik sebanyak 175 siswa
Rumus Diagram Lingkaran dalam Bentuk Persen (%)
Pada kasus ini, data yang diketahui berbentuk persen (%). Di beberapa soal, diagram lingkaran dalam bentuk persen sering di jumpai. Untuk dapat menyelesaikan soal dalam bentuk persen, jika yang di tanyakan adalah jumlah angka, pertama cari terlebih dahulu persen dari data yang di tanyakan kemudian kalikan dengan total jumlah nilai setelah itu bagikan dengan 100% (total persen).
Baca Juga : Cara menghitung Persen (%)
Rumus:
Nilai yang ditanyakan = (persen nilai yang ditanyakan/100%) x total nilai
Contoh soal
Diketahui total barang yang dijual pedagang baju adalah 300 buah. Jika baju yang dijual dibentuk dalam diagram lingkaran sebagai berikut:
Carilah berapa baju anak yang dijual pedagang baju tersebut?
Jawab:
Diketahui:
Total baju = 300 buah
Baju remaja = 40%
Baju dewasa = 38%
Ditanyakan:
Banyaknya baju anak yang di jual ... ?
Penyelesaian:
Pertama-tama, cari berapa persen baju anak yang di jual.
persen baju anak = 100% - (baju remaja + baju dewasa)
= 100% - (40% + 38%)
= 100% - 78%
= 22%
Kemudian, gunakan persen baju anak yang di dapatkan kedalam rumus.
Jumlah baju anak = (persen baju anak/100%) x total baju
= (22% / 100%) x 300 buah
= 6600/100
= 66 buah
Jadi, jumlah baju anak yang dijual pedagang baju adalah 66 buah
Teori Perbandingan (Sering digunakan dalam diagram lingkaran)
Pada teori ini, dapat digunakan pada diagram lingkaran dalam bentuk derajat dan dalam bentuk persen. Teori perbandingan sangat membantu untuk menemukan nilai yang di cari jika yang diketahui sangat sedikit. Perhatikan penjelasan berikut:
Misalkan yang diketahui A dan B:
persen A = nilai A atau derajat A = nilai A
persen B = nilai B atau derahat B = nilai B
Dari data diatas dapat dilakukan perbandingan A dengan B
maka untuk dapat mencari nilai, diantaranya:
nilai A = (persen A/persen B) x nilai B
atau
nilai A = (derajat A/derajat B) x nilai B
nilai B = (persen B/persen A) x nilai A
atau
nilai B = (derajat B/derajat A) x nilai A
untuk mencari persen atau derajat, diantaranya:
persen A = (nilai A/nilai B) x persen B
atau
derajat A = (nilai A/nilai B) x derajat B
persen B = (nilai B/nilai A) x persen A
atau
derajat B = (nilai B/nilai A) x derajat A
Contoh soal penggunaan Teori perbandingan dalam diagram lingkaran
Sebuah sekolah memiliki data-data siswa yang mengikuti kegiatan eskul dalam bentuk diagram lingkaran sebagai berikut:
Jika jumlah siswa yang mengikuti eskul bola sebanyak 450 siswa, berapakah siswa yang mengikuti eskul voli?
Jawab:
Diketahui:
persen eskul bola = 45 %
persen eskul voli = 25 %
jumlah eskul bola = 450 siswa
Ditanyakan:
Banyaknya siswa yang mengikuti eskul voli ... ?
Penyelesaian:
jumlah eskul voli = (persen eskul voli/persen eskul bola) x jumlah eskul bola
= (25% / 45%) x 450
= 11250/45
= 250 siswa
Jadi, jumlah siswa yang mengikuti eskul voli adalah 250 siswa
Kesimpulan:
- Diagram lingkaran merupakan diagram yang digunakan untuk mempermudah dalam melihat data-data yang biasa digunakan untuk mendeskripsikan berapa besar data dan perbadingan data yang satu dengan yang lainnya.
- Untuk menggunakan rumus, perhatikan jenis soal dan perhatikan nilai yang diketahui.
- Ada beberapa jenis soal diagram lingkaran yang sering muncul dalam soal, diantaranya diagram liangkaran biasa (dalam bentuk angka), diagram lingkaran dalam bentuk persen, dan diagram lingkaran dalam bentuk derajat.
- Teori perbandingan digunakan apabila nilai yang diketahui (jumlah) dan bentuk nilai (dalam persen atau derajat) ada.
Demikianlah beberapa penjelasan mengenai Cara Menghitung, Rumus Diagram Lingkaran serta Contoh. Jika anda memiliki pertanyaan seputar materi di atas, silahkan tinggalkan pertanyaan anda di papan komentar yang ada di bawah. Kami akan berusaha untuk menjawab semua pertanyaan anda. Semoga bermanfaat.
Sumber : Matematika SMA



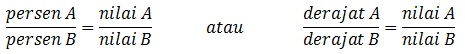

Berguna
ReplyDeleteBagus
terima kasih :)
DeleteThank you
ReplyDeletesangat membantu, terimakasih
ReplyDeleteapakah cara mencari diagram yang berbentuk derajat sama dengan persen yang ditunjukkaan pada contoh terakhir
ReplyDeleteberbeda. Total persen yaitu 100% sedangkan derajar yaitu 360 derajad lingkrang penuh.
DeleteTerima Kasih karna sangat membantu
Deletemakasyyii
ReplyDeletebagaimana jika yang diketahui hanya dari dua juring yang ada sedang soalnya di tanyakan jumlah juring yang lain?
ReplyDeletesaya kurang paham dengan pertanyaannya. Coba berikan 1 contoh kasus.
DeleteTerima kasih karena sangat membantu
Deletejika yag diketahui perse bagaimana cara mencari eskul nya
ReplyDeletePersen yang bagaimana? tolong jelaskan lebih terperinci soalnya bagaimana. :)
Delete